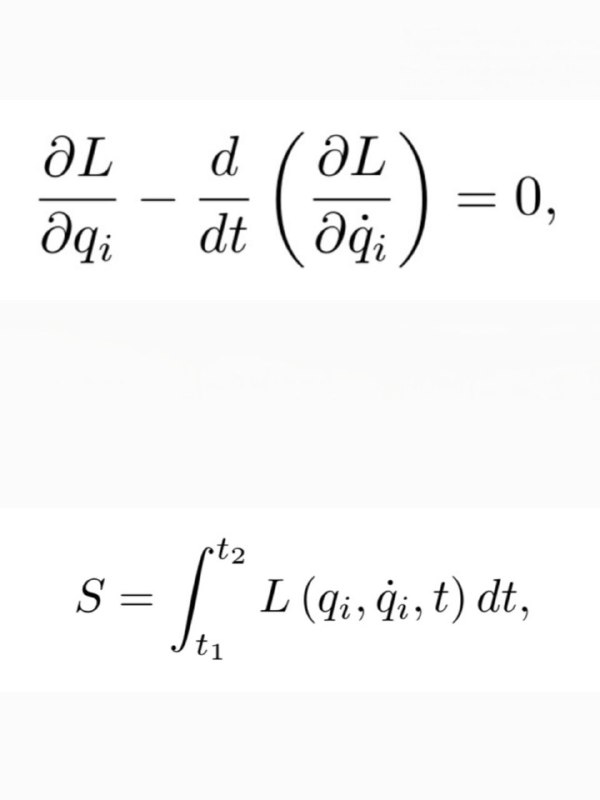با نوشتن قانون دوم نیوتن در مختصات عمومی q(x,y,z) میتوان معادلات حرکت لاگرانژ را بدست آورد. (معادله۱)
این معادله با مینیمم کردن تابع کنش S بدست میآید. (معادله۲) که به آن اصل حداقل کنش گفته میشود. این معادله ساده کل مکانیک کلاسیک را در بر دارد و علاوه بر ذرات با استفاده از آن میتوان میدانها را نیز توصیف کرد.
اصل کمترین کنش بیان میکند که در بین بینهایت مسیر بین دو نقطه، ذره کلاسیکی مسیری را انتخاب میکند که در آن کنش کمینه باشد.
فاینمن با ایده گرفتن از اصل کمترین کنش مکانیک کلاسیک، فرمولبندی مکانیک کوانتوم را با انتگرال مسیر انجام داد. جنس احتمالاتی مکانیک کوانتوم موجب میشود که تمام مسیرهای بین A و B ممکن باشد و به هرکدام احتمالی اختصاص مییابد.
جالب آنکه مسیر کلاسیکی که از اصل کمترین کنش بدست میآید، مسیری است که در مکانیک کوانتوم محتملترین است.
🆔 @Physics3p
>>Click here to continue<<