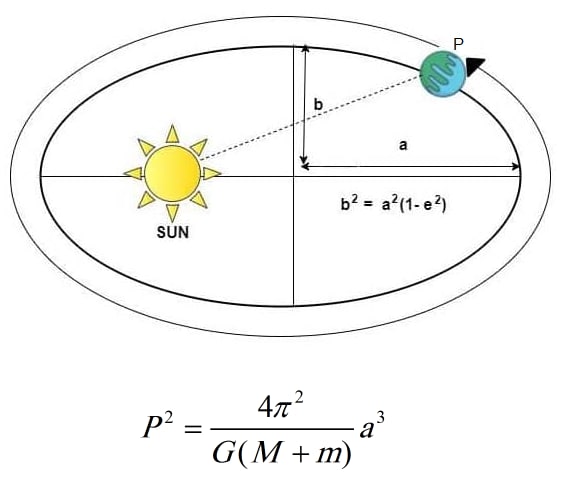
🟠 استخراج قانون سوم کپلر
حال در موقعیتی قرار گرفته ایم که می توانیم با استفاده از دو قانون قبل، قانون سوم کپلر را هم استخراج کنیم. با انتگرال گیری از قانون دوم کپلر (dA/dt = L/2μ) در یک دوره تناوب P خواهیم داشت:
A=(L/2μ)P
در اینجا، جسم m که به دور جسم ثابت و بسیار بزرگتر M می گردد با جرم کاهیده ی μ که حول مرکز جرم می گردد تعویض شده است. با جای گذاری مساحت بیضی (A=πab) و به توان 2 رساندن طرفین معادله و چیدمان مجدد، به رابطه ی ذیل می رسیم:
P^2 = 4π^2 a^2 b^2 μ^2 / L^2
سر انجام با استفاده از معادله b^2 = a^2(1-e^2) و رابطه تکانه ی زاویه ای کل (معادله ی آخر قانون اول کپلر)، معادله ی آخر به صورت ذیل ساده می شود:
P^2 = 4π^2 a^3/G(m1 + m2)
این رابطه شکل عمومی قانون سوم کپلر (در برخی منابع علمی به نام قانون سوم کپلر به شکل نیوتونی نیز معروف می باشد) است. نیوتون نه تنها رابطه ای میان نیم محور اصلی مدار بیضی و تناوب مداری را ثابت نمود، بلکه شرطی را یافت که کپلر به طور تجربی موفق به کشف آن نشده بود و آن این است که مربع تناوب مداری با جرم کل منظومه نسبت عکس دارد. در این باره هم باید از خطای کپلر به خاطر عدم توجه به این اثر چشم پوشی کرد. اولین علت بروز چنین خطایی این بود که اطلاعات تیکو فقط به منظومه ی شمسی ما محدود میشد. علت دیگر هم این بود که در منظومه ی شمسی جرم خورشید بسیار بزرگتر از جرم هر سیاره ی دیگری است یعنی:
Ms + mp = Ms
اگر P را بر حسب سال و a را بر حسب واحد نجومی در نظر بگیریم، مقدار مجموعه ی ثوابت (از جمله جرم خورشید) برابر با یک خواهد شد (در سال 1621 کپلر توانست ثابت کند که چهار قمر گالیله ای مشتری هم از قانون سوم P^2 = ka^3 تبعیت می کنند. در این رابطه دیگر k، برابر یک نیست. اما کپلر نمی دانست که در مورد جسم مورد بحثش k برابر یک نسیت). این قانون آسان ترین راه برای به دست آوردن جرم اجرام آسمانی است؛ از همین رو در درک بهتر بسیاری از پدیده های سماوی، نقش مثمر ثمری ایفا می کند. در صورت کلی قوانین کپلر که از قوانین نیوتون استخراج می شود، علاوه بر سیاره هایی که به دور خورشید می گردند؛ در مورد مدار های کهکشان-کهکشان هم صدق می کند. با دانستن دوره تناوب مداری و نیم محور اصلی بیضی، می توان جرم کل منظومه را به دست آورد.
🔺منبع: کتاب مقدمه ای بر اخترفیزیک نوین "بردلی کارول - دیل اوستلی"
🆔@physics3p
>>Click here to continue<<