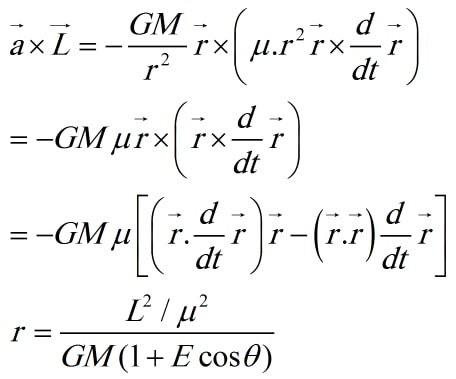🟠 قانون اول کپلر
▫️تعریف: هر سیاره در مداری بیضی شکل به دور خورشید می گردد، به طوری که خورشید در یکی از کانون های این بیضی قرار گرفته است.
▪️استخراج: برای استخراج قوانین کپلر؛ ابتدا باید اثر گرانش را بر تکانه زاویه ای مداری سیاره بررسی کنیم. با استفاده از مختصات مرکز جرم و محاسبه ی مشتق زمانی از تکانه ی زاویه ای جرم کاهیده(μ=m1m2/(m1 + m2)) در مدار (L = μ.r × v = r ×p)، خواهیم داشت:
dL/dt = dr/dt ×p + r × dp/dt = v × p + r × F
عبارت دوم، از تعریف سرعت و قانون دوم نیوتون نتیجه شده است. توجه داشته باشید از آنجا که v و p هم جهت هستند، ضرب برداریشان صفر خواهد شد. به همین ترتیب، چون F نیرویی مرکزگرا در امتداد r و به سمت داخل است، ضرب برداری r و F هم صفر خواهد شد.
نتیجه ی این معادله قاعده ای مهم و کلی در مورد تکانه ی زاویه ای است:
dL/dt = 0
به عبارتی می توان گفت در سیستم هایی که نیرو مرکزگرا است، تکانه ی زاویه ای همواره ثابت باقی می ماند.
با استفاده از بردار واحد (یکه) شعاعی (r=rr)، می توانیم بردار تکانه ی زاویه ای را به شکل دیگری بازنویسی کنیم:
L = μr × v = μrr × d(rr)/dt =μrr × (dr/dt)r + r(d/dt)r = μr^2r × (d/dt)r
نتیجه ی آخر، از این نکته که r×r = 0 است ناشی می شود. شتاب جرم کاهیده که ناشی از نیروی گرانش اعمال شده از سوی جسم M اس، در شکل برداری به این صورت در می آید:
a = -(GM/r^2)r
با نوشتن ضرایب برداری بین شتاب جرم کاهیده و تکانه ی زاویه ای مداری اش خواهیم داشت:
a × L = -(GM/r^2)r × (μ.r^2 r × (d/dt)r) = -GMμr × (r × (d/dt)r)
و با به کار گیری اتحاد برداری A × (B × C) = (A.C)B - (A.B)C، داریم:
a × L = -GMμ[ (r.(d/dt)r - (r.r)(d/dt)r ]
از آنجا که ^r، برداری واحد است؛ r^.r^=1:
d/dt(r.r) = 2r.(d/dt)r = 0
و در نتیجه:
a × L =GMμ(d/dt)r
(d/dt)(v × L) = (d/dt)(GMμ.r)
در این صورت با انتگرال گیری بر حسب زمان، چنین به دست می آوریم:
v × L =GMμr + D *
که D برداری ثابت است. از آنجا که v × L و ^r هر دو در یک صفحه ی مداری قرار دارند، D هم باید منطبق بر همین صفحه باشد. به علاوه مقدار طرف چپ رابطه، در حضیض مداری (کمترین فاصله از کانون) به حالت بیشینه ی خود می رسد (زمانی که سرعت جرم کاهیده در بیشینه است). از طرف دیگر، زمانی که r و D هم جهت باشند، مقدار سمت راست عبارت بیشترین مقدار را خواهد داشت. بنابراین D به سوی حضیض جابجا می شود. همانطور که در ذیل نشان داده شده است؛ مقدار عددی D، خروج از مرکز مدار را تعیین می کند.
حال حاصل ضرب نقطه ای بردار معادله ی * در بردار مکان، r را به صورت rr می نویسیم:
r.(v × L) = GMμrr.r + r.D
با استفاده از اتحاد برداری A.(B × C) = (A ×B).C، خواهیم داشت:
(r × v).L = GMμ.r + rDcosθ
در آخر با یاد آوری تعریف تکانه ی زاویه ای، خواهیم داشت:
L^2/μ = GMμr(1 + Dcosθ/GMμ)
که θ زاویه ی جرم کاهیده نسبت به حضیض مداری است. با تعریف e = D/GMμ و با حل معادله بر حسب r، خواهیم داشت:
r = (L^2/μ^2)/GM(1 + ecosθ)
که همان قانون اول کپلر است.
🔸در این متن حروف bold شده نماد بردار می باشند.
🔺منبع: کتاب مقدمه ای بر اخترفیزیک نوین "بردلی کارول - دیل اوستلی"
🆔@physics3p
>>Click here to continue<<