🟢 توزیع ماکسول-بولتزمن
برای درک بهتر مبنای فیزیکی طبقه بندی طیفی ستارگان، باید به دو سوال پایه ای پاسخ داد: احتمال یافتن الکترون ها در چه اوربیتال (مدار) هایی بیشتر است؟ اتم ها در مراحل مختلف یونش با چه اعداد نسبی ای مشخص می شوند؟
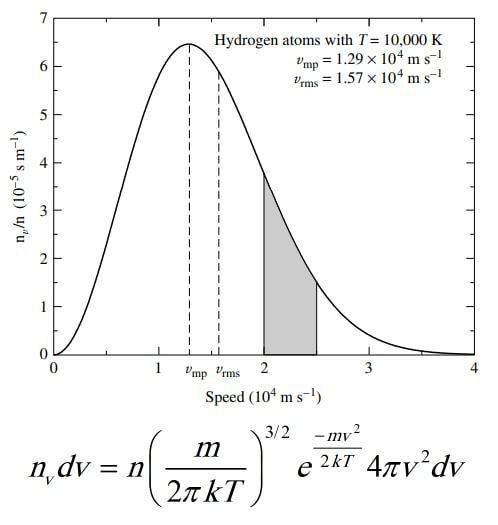
پاسخ هر دوی این سوال ها در شاخه ای از فیزیک که به مکانیک آماری معروف است، تحلیل می شود. این شاخه از فیزیک، ویژگی های آماری سیستمی که متشکل از چندین عضو است را بررسی می کند. برای مثال یک گاز می تواند حاوی تعداد زیادی از ذرات با سرعت ها و انرژی های متفاوتی باشد. هر چند که در عمل، مطالعه ی رفتار دقیق هر ذره به صورت مجزا امکان پذیر نیست اما کل گاز به صورت مجموعه ای واحد، ویژگی های تعریف شده و خاصی مثل دما، فشار و چگالی را داراست. برای چنین گازی که در تعادل گرمایی قرار دارد (دمای گاز به سرعت کاهش یا افزایش نمی یابد)، تابع توزیع ماکسول-بولتزمن کسری از ذرات با دامنه ی مشخصی از سرعت را تعیین می کند. تعداد ذراتی از گاز که در واحد حجم سرعتی بین v و v+dv دارند؛ توسط فرمول موجود در تصویر محاسبه می شود.
🔺که در آن n چگالی عددی کل (تعداد کل ذرات بر واحد حجم)، nv= ∂n/∂v و m جرم هر ذره، k ثابت بولتزمن و T دمای گاز بر حسب کلوین است.
تصویر موجود، توزیع سرعت های مولکولی را بر حسب کسری از مولکول هایی که سرعتی بین v و v+dv دارند، نشان می دهد. توزیع این سرعت ها از تابع ماکسول-بولتزمن پیروی می کند. بخش نمایی تابع توزیع، نسبت انرژی جنبشی ذرات گاز یعنی 1/2mv^2، به انرژی گرمایی یا kT را مشخص می نماید. بدیهی است که داشتن انرژی های بسیار بیشتر یا کمتر از انرژی گرمایی کل برای تعداد زیادی از ذرات، بسیار دشوار یا تقریبا محال است. هنگامی که این انرژی ها مساوی باشند تابع توزیع سرعت، به بیشینه ی (قله)خود می رسد. تساوی این انرژی ها در یک سرعت بیشینه موسوم به سرعت محتمل (vmp) که به صورت زیر تعریف می شود، رخ می دهد:
vmp^2 = 2kT/m
برای به دست آوردن سرعت میانگین ذرات، دنباله ی نمایی تابع توزیع؛ مقدار بزرگ تری را برای سرعت نتیجه می دهد که به سرعت ربشه ی میانگین مربعی (vrms) هم موسوم است و چنین بدست می آید:
vrms^2 = 3kT/m
🔺منبع: کتاب مقدمه ای بر اخترفیزیک نوین "بردلی کارول - دیل اوستلی"
🆔@physics3p
>>Click here to continue<<