🟠 تابش جسم سیاه (قسمت سوم) (قسمت پایانی)
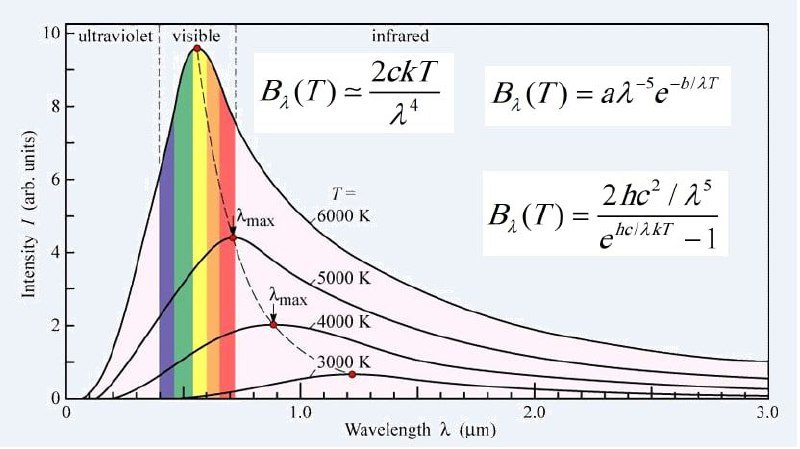
سرانجام در اواخر سال 1900 یک فیزیک دان آلمانی به نام ماکس پلانک (1947-1857) دریافت که می توان قانون وین را طوری اصلاح نمود تا طیف های جسم سیاه با دقت زیادی با آن چه در نمودار تابش جسم سیاه می بینید، مطابقت داشته باشد و در عین حال قانون ریلی-جینز هم در مورد طول موج های بلند درست عمل کند و به فاجعه ی فرابنفش منجر نشود:
Bλ (T) = (a/λ^5)/(e^(b/λT)-1)
پلانک برای تعیین ثوابت a و b، ضمن جلوگیری از فاجعه ی فرابنفش، از یک حقه ی ریاضی زیرکانه استفاده کرد. وی چنین فرض نمود که یک موج ایستای الکترومغناطیس با طول موج λ و فرکانس v=c/λ نمی تواند هر مقدار از انرژی قرار دادی را بدست آورد. بلکه، تنها می تواند مقادیر انرژی مجاز و خاصی را داشته باشد که مضارب صحیحی از انرژی موج کمینه هستند (در واقع پلانک، انرژی های ممکن برای تابش الکترومغناطیس فرضی را که از دیواره های اجاق گسیل می شدند محدود کرد). این انرژی کمینه، یعنی یک کوانتوم انرژی با رابطه hv یا hc/λ به دست می آید و h هم در اینجا یک ثابت است (ثابت پلانک). بنابراین انرژی یک موج الکترومغناطیس nhv یا nhc/λ است که n عددی صحیح و عدد کوانتومی موج را نشان می دهد. با در نظر گرفتن این بسته های کوانتیده شده انرژی، (موجی کوانتیده همراه با انرژی کمینه ای که با فرکانس موج متناسب است) حتی کل اجاق هم نمی تواند، انرژی کافی برای تامین حتی یک کوانتوم انرژی برای امواجی با طول موج کوتاه و فرکانس بالا را تامین کند. در نتیجه جلوی فاجعه ی فرابنفش گرفته می شود.
پلانک امیدوار بود که در پایان محاسباتش، ثابت h برابر صفر شود؛ مطمئنا در نتیجه ی پایانی وی برای Bλ (T)، نمی بایست ثابتی مصنوعی وجود داشته باشد. تدبیر پلانک موثر واقع شد! فرمول وی که اکنون تابع پلانک نامیده می شود به طور حیرت آوری با آزمایش ها مطابقت می کند، (اما در صورتی که ثابت h در معادله باقی بماند).
Bλ (T) = (2hc^2/λ^5)/(e^(hc/λkT)-1)
▫️مقدار ثابت پلانک h= 6.62606876 x 10^34 Js است.
🔺منبع: کتاب مقدمه ای بر اخترفیزیک نوین "بردلی کارول - دیل اوستلی"
🆔@physics3p
>>Click here to continue<<