🟠 تابش جسم سیاه (قسمت اول)
هر کس که در یک شب صاف زمستانی به صورت فلکی جبار (شکارچی) نگاه کرده باشد، متوجه رنگ های شاخص ابط الجوزای سرخ فام (در شانه ی شمار شرقی جبار) و رجل الجبار آبی-سفید (در پای جنوب غربی) این صورت فلکی شده است. این رنگ ها حاکی از تفاوت دمای سطح این دو ستاره است. دمای سطحی ابط الجوزا حدود 3600k است و بسیار سرد تر از دمای سطح رجل الجبار است که 13000k می رسد.
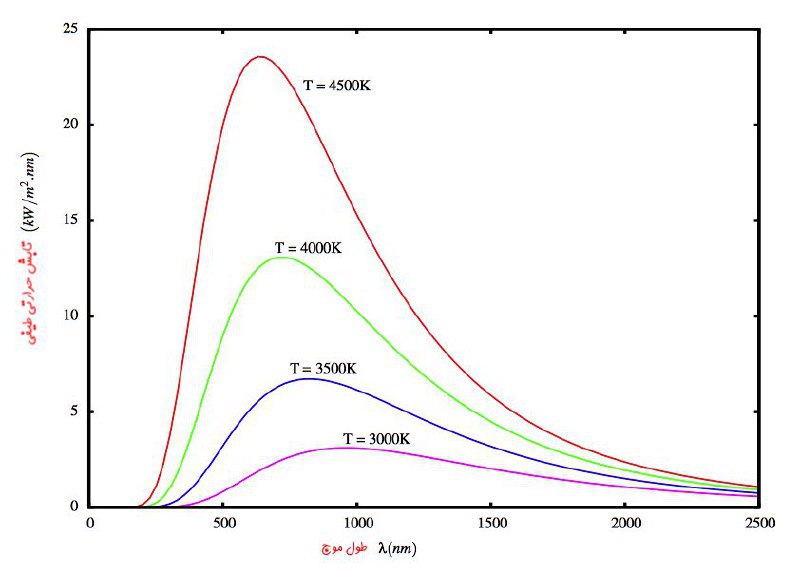
ارتباط میان رنگ نور گسیل شده از یک جسم داغ با دمای آن نخستین بار در سال 1792 مورد توجه مخترع انگلیسی، توماس وج وود (Thomas Wedgewood) قرار گرفت. تمامی کوره هایی که وج وود آزمایش های خود را بر آن ها متمرکز کرده بود، با هر شکل و ساختاری، در یک دمای خاص به رنگ سرخ می درخشیدند. بررسی های بعدی فیزیک دانان نشان داد که هر جسمی با دمای بالای صفر مطلق در تمامی طول موج ها، با شدت های مختلفی نور گسیل می کند. وی فهمید که یک گسیل کننده ی ایده آل جسمی است که تمامی انرژی نورانی فرود آمده بر خود را جذب کرده و این انرژی را با طیف مشخصه ی نشان داده شده در شکل بازتاب نماید. از آنجا که یک گسیل کننده ی ایده آۀ، هیچ نوری را منعکس نمی کند، به آن جسم سیاه می گویند و تابشی را که از آن گسیل می شود، تابش جسم سیاه می نامند. امروزه می دانیم که با دقت بسیار خوبی می توان ستارگان را جسم سیاه در نظر گرفت.
▫️طیف جسم سیاه در طول موج λmax به بیشینه ی خود می رسد و با افزایش دما این طول موج کوتاه تر می شود. رابطه بین λmax و T به قانون جابجایی وین مشهور است:
T.λmax= 0.002897755 mk
🔺معادله ی استفان-بولتزمن
شکل تابش جسم سیاه همچنین نشان می دهد که با افزایش دمای جسم سیاه، در هر ثانیه انرژی بیشتری (در تمامی طول موج ها) گسیل می شود. آزمایش هایی که فیزیک دان اتریشی، ژوزف استفان (1893-1835) در سال 1879 انجام داد ثابت کرد که درخشندگی کل L برای جسم سیاهی با مساحت سطح A و دمای T (بر حسب کلوین) به صورت ذیل به دست می آید:
L = AσT^4
پنج سال بعد، فیزیک دان اتریشی دیگری به نام لودویگ بولتزمن (1906-1844) با استفاده از قوانین ترمودینامیک و فرمول ماکسول برای فشار تابشی، این معادله را که امروزه به معادله ی استفان-بولتزمن معروف است، استخراج نمود. مقدار عددی ثابت استفان-بولتزمن σ، چنین است:
σ= 5.6704 x 10^-8 Wm^-2k^-4
برای یک ستاره کروی به شعاع R و مساحت سطح A= 4πR^2، معادله ی استفان-بولتزمن به صورت زیر در می آید:
L= 4πR^2σTe^4
از آنجا که ستارگان دقیقا مشابه جسم سیاه رفتار نمی کنند، ما از این معادله برای تعریف دمای موثر سطح ستاره (Te)، استفاده می کنیم. ترکیب این معادله با قانون عکس مجذوری (رابطه عکس مجذور فاصله با تابش) ثابت می کند که در فاصله ی سطح ستاره (r=R)، شار سطحی (بر حسب وات بر متر مربع) به این صورت خواهد بود:
Fسطح= σTe^4
🔺منبع: کتاب مقدمه ای بر اخترفیزیک نوین "بردلی کارول - دیل اوستلی"
🆔@physics3p
>>Click here to continue<<