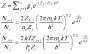🔴 معادله ساها
❓سوالی که در بررسی طیف ستارگان بوجود می آید این است که بع عنوان مثال، چرا خطوط بالمر در دمایی بسیار پایین تر از 9520K به بیشینه ی شدت خود می رسد؟ طبق معادله ی بولتزمن، واضح است که در دما های بالاتر از 9520K، بخش بیشتری از الکترون ها به جای تراز پایه، در نخستین تراز برانگیختگی خواهند بود. اگر این طور باشد، چه چیزی مسئول کاهش شدت خطوط بالمر در دما های بالاتر است؟
▫️پاسخ این پرسش در نسبت اتم های موجود در تراز های مختلف یونش نهفته است. فرض کنید Xi انرژی یونش مورد نیاز برای کندن یک الکترون از یک اتم (یا یون) در تراز پایه باشد، تا آن را از درجه ی یونش i به درجه ی یونش (i+1) برساند.
برای مثال، انرژی یونش هیدروژن، یعنی انرژی لازم برای تبدیل هیدروژن خنثی به هیدروژن یک بار یونیده (HI => HII)، برابر است با Xi= 13.6 ev است. تقسیم مجموع انرژی الکترون های هر اتم بر تعداد تراز ها، میانگین انرژی تراز ها را به دست می دهد. این روند به محاسبه ی تابع پارش (Partition Function) Z بر حسب اتم های اولیه و نهایی می انجامد. تابع پارش را می توان میانگین وزنی تمامی تراز هایی در نظر گرفت که؛ یک اتم می تواند الکترون هایی با انرژی های یکسان را در فضا بپیند. اگر Ej تراز انرژی j ام و gi واگنی آن تراز باشد، تابع پارش Z به صورت رابطه اول تعریف می شود.
اگر تابع پارش Zi و Z(i+1) را برای اتمی در مراحل اولیه و پایانی یونش بنویسیم، نسبت تعداد اتم ها در مرحله ی یونش i+1 به تعداد اتم ها در مرحله ی یونش i، به رابطه دوم خواهیم رسید.
این معادله به معادله ی ساها معروف است. اخترفیزیک دان هندی مگاند ساها (Meghnad Saha) (1894-1956)، در سال 1920 برای نخستین بار به این معادله دست یافت. از آن جا که در طی فرآیند یونش، یک الکترون آزاد می شود؛ مشاهده ی چگالی عددی الکترون های آزاد (تعداد الکترون ها در واحد حجم) یا ne در سمت راست معادله ی ساها چندان عجیب نیست. توجه داشته باشید که با افزایش چگالی عددی الکترون های آزاد، تعداد اتم ها در مراحل بالاتر یونش کاهش می یابد، زیرا الکترون های بیشتری وجود دارد که یون می تواند دوباره با آن ها ترکیب شود. ضریب 2 در کنار تابع پارش Z(i+1)؛ وجود دو اسپین قابل پذیرش برای الکترون های آزاد با ms= +- 0.5 را نشان می دهد. عبارت موجود در پرانتز هم به الکترون آزاد مربوط است (عبارت داخل پرانتز، چگالی عددی الکترون هایی با انرژی کوانتومی برابر با انرژی گرمایی kT را نشان می دهد. برای شرایط متداول در جو های ستاره ای، این عبارت خیلی بزرگتر از ne است.) و me هم جرم الکترون را نشان می دهد.
گاهی به جای استفاده از چگالی عددی الکترون از فشار الکترون های آزاد یا Pe استفاده می شود. فشار الکترون های آزاد با کمک از قانون گاز کامل ایده آل، به این صورت محاسبه می شود:
Pe = nekT
با استفاده از تعریف جدید، معادله ی ساها را به صورت رابطه سوم بازنویسی می کنیم.
🔺منبع: کتاب مقدمه ای بر اخترفیزیک نوین "بردلی کارول - دیل اوستلی"
🆔@physics3p
>>Click here to continue<<