Schubert polynomials, pipe dreams and Fomin-Kirillov theorem
Valentina Kiritchenko, HSE University (Moscow, Russia)
Abstract: In these lectures, we discuss combinatorial aspects of Schubert varieties. Connections with Schubert calculus and enumerative geometry will also be outlined. A more detailed description is provided below.
Lecture 1: Enumerative geometry and Schubert polynomials
How many lines intersect four given lines in a 3-space? And how many lines lie on a cubic surface? Schubert calculus helps to solve these classical problems and many others. Grassmann, flag and Schubert varieties play an important role in Schubert calculus. We discuss Schubert polynomials – algebraic counterparts of Schubert varieties – and their applications to enumerative geometry.
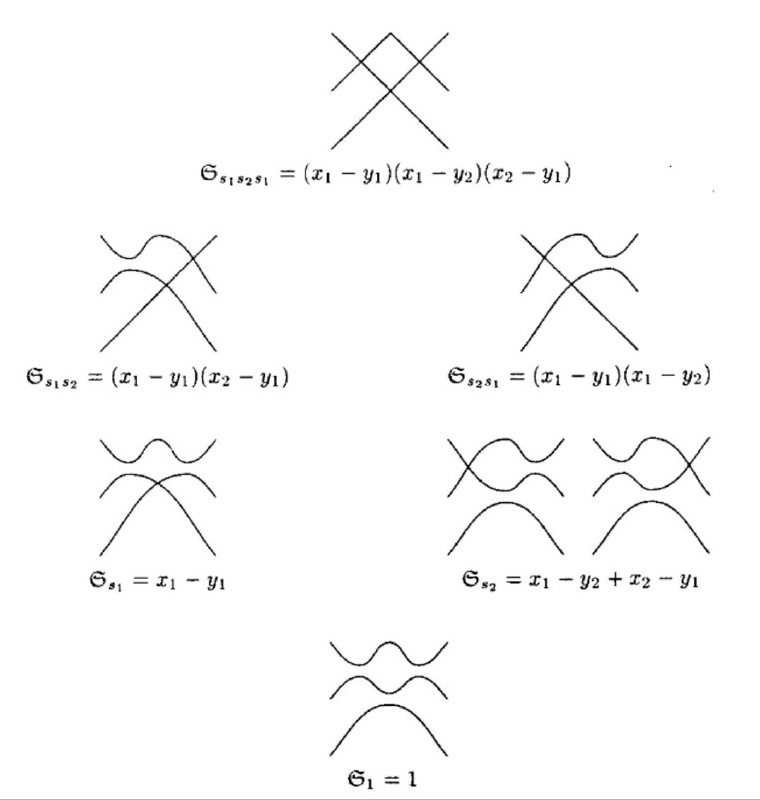
Lecture 2: Pipe dreams and Fomin-Kirillov theorem
Schubert polynomials admit a positive description using combinatorial objects called pipe dreams. Classical pipe dreams of Fomin-Kirillov realize permutations of n elements. There are also more recent versions of pipe dreams by Fujita-Nishiyama for signed permutations of 2n elements. We define pipe dreams and discuss their applications to Schubert calculus.
Prerequisites: Linear algebra and some basics of abstract algebra. Familiarity with rudiments of topology is desirable, but not essential.
Расписание лекций см. выше
>>Click here to continue<<