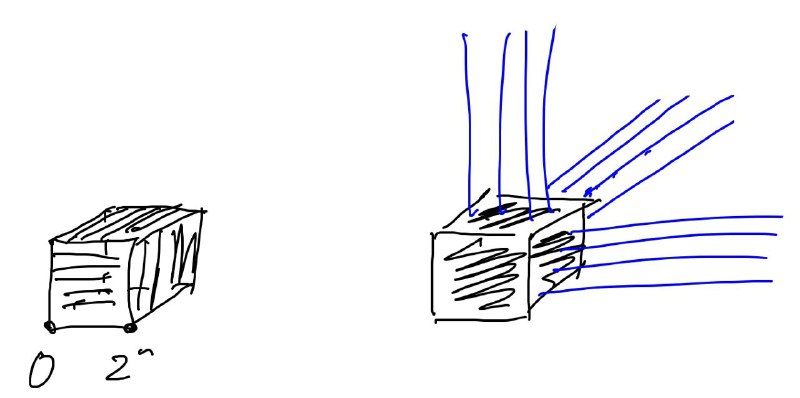
Давайте я продолжу (и попробую закончить) историю про ним с тремя кучками камней — или, что то же самое, про игру "ладью в угол" в кубе.
Мы выше видели, что в кубе размера 1,2,4,8 возникает по одной проигрышной позиции в каждом столбце. И хочется сказать, что так же будет для куба любого размера 2^n.
Это оказывается несложно (и очень естественно) доказать просто по индукции.
Действительно — если это так для какого-то размера куба N=2^n, то на продолжениях этих столбцов все позиции оказываются выигрышными. И из-за симметрии так будет в каждом из трёх направлений (см. рис.).
>>Click here to continue<<