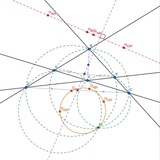
№32 (ВсОШ ЗЭ 2013, 11.7)
Окружность с центром I, вписанная в треугольник ABC, касается сторон BC, CA, AB в точках A1, B1, C1 соответственно. Пусть Ia, Ib, Ic — центры вневписанных окружностей треугольника ABC, касающихся соответственно сторон BC, CA, AB. Отрезки IaB1 и IbA1 пересекаются в точке C2. Аналогично, отрезки IbC1 и IcB1 пересекаются в точке A2, а отрезки IcA1 и IaC1 — в точке B2. Доказать, что I является центром окружности, описанной около треугольника A2B2C2.
>>Click here to continue<<