№27 (ВсОШ ЗЭ 2015, 11.7)
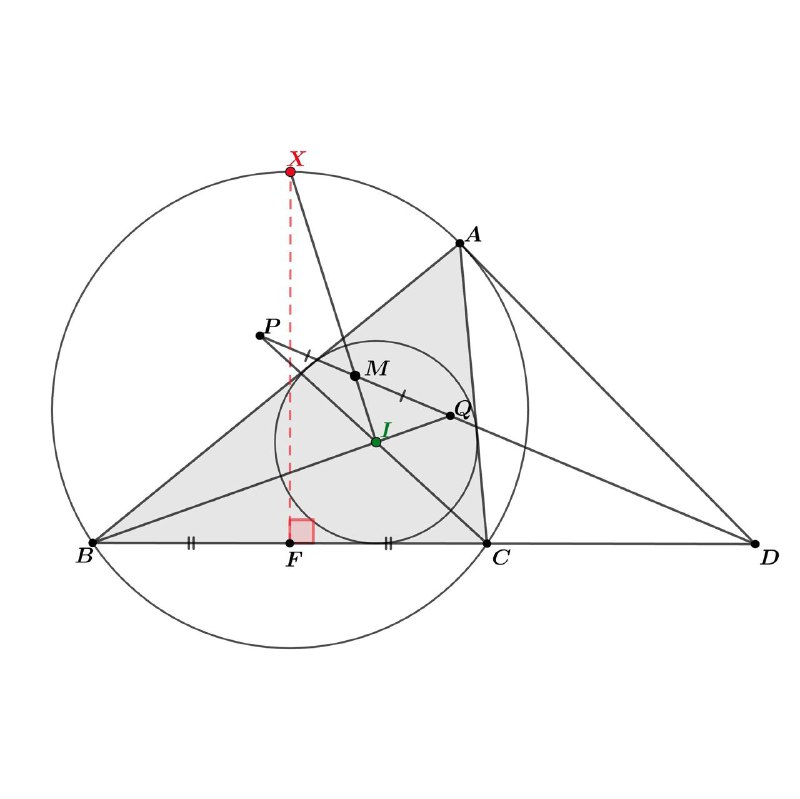
Неравнобедренный треугольник ABC вписан в окружность ω. Касательная к этой окружности в точке А пересекает прямую ВС в точке D. Пусть I — центр окружности, вписанной в треугольник ABC. Прямые BI и CI пересекают биссектрису угла ADB в точках Q и P соответственно. Пусть M — середина отрезка PQ.
Доказать, что прямая MI проходит через
середину дуги ACB окружности ω
Bitcoin is a decentralized digital currency that you can buy, sell and exchange directly, without an intermediary like a bank. Bitcoin’s creator, Satoshi Nakamoto, originally described the need for “an electronic payment system based on cryptographic proof instead of trust.” Each and every Bitcoin transaction that’s ever been made exists on a public ledger accessible to everyone, making transactions hard to reverse and difficult to fake. That’s by design: Core to their decentralized nature, Bitcoins aren’t backed by the government or any issuing institution, and there’s nothing to guarantee their value besides the proof baked in the heart of the system. “The reason why it’s worth money is simply because we, as people, decided it has value—same as gold,” says Anton Mozgovoy, co-founder & CEO of digital financial service company Holyheld.
With Telegram, you can send messages, photos, videos and files of any type (doc, zip, mp3, etc), as well as create groups for up to 200,000 people or channels for broadcasting to unlimited audiences. You can write to your phone contacts and find people by their usernames. As a result, Telegram is like SMS and email combined — and can take care of all your personal or business messaging needs. In addition to this, we support end-to-end encrypted voice calls.
Telegram is a messaging app with a focus on speed and security, it’s super-fast, simple and free. You can use Telegram on all your devices at the same time — your messages sync seamlessly across any number of your phones, tablets or computers.
Telegram is for everyone who wants fast and reliable messaging and calls. Business users and small teams may like the large groups, usernames, desktop apps and powerful file sharing options. You can appoint admins with advanced tools to help these communities prosper in peace. Public groups can be joined by anyone and are powerful platforms for discussions and collecting feedback.In case you're more into pictures, Telegram has animated gif search, a state of the art photo editor, and an open sticker platform (find some cool stickers here or here). What's more, there is no need to worry about disk space on your device. With Telegram's cloud support and cache management options, Telegram can take up nearly zero space on your phone.
Unlike WhatsApp, Telegram is a cloud-based messenger with seamless sync. As a result, you can access your messages from several devices at once, including tablets and computers, and share an unlimited number of photos, videos and files (doc, zip, mp3, etc.) of up to 2 GB each. And if you don't want to store all that data on your device, you can always keep it in the cloud.Thanks to our multi-data center infrastructure and encryption, Telegram is faster and way more secure. On top of that, Telegram is free and will stay free — no ads, no subscription fees, forever.
Yes! Voice calls are currently available to users around the world.
Many modern travelers appear to struggle with managing various aspects of their finances simultaneously while abroad, such as banking, budgeting, investing, trading, and saving. It is important to have apps installed on the device that will help you carry out these necessary tasks.
Hot Topic in US